Ji-An, L., Benna, M.K. & Mattar, M.G. Discovering cognitive strategies with tiny recurrent neural networks. Nature (2025)
Li Ji-An, Marcus K. Benna ,Marcelo G. Mattar
Understanding how animals and humans learn from experience to make adaptive decisions is a fundamental goal of neuroscience and psychology. Normative modelling frameworks such as Bayesian inference1 and reinforcement learning2 provide valuable insights into the principles governing adaptive behaviour. However, the simplicity of these frameworks often limits their ability to capture realistic biological behaviour, leading to cycles of handcrafted adjustments that are prone to researcher subjectivity. Here we present a novel modelling approach that leverages recurrent neural networks to discover the cognitive algorithms governing biological decision-making. We show that neural networks with just one to four units often outperform classical cognitive models and match larger neural networks in predicting the choices of individual animals and humans, across six well-studied reward-learning tasks. Critically, we can interpret the trained networks using dynamical systems concepts, enabling a unified comparison of cognitive models and revealing detailed mechanisms underlying choice behaviour. Our approach also estimates the dimensionality of behaviour3 and offers insights into algorithms learned by meta-reinforcement learning artificial intelligence agents. Overall, we present a systematic approach for discovering interpretable cognitive strategies in decision-making, offering insights into neural mechanisms and a foundation for studying healthy and dysfunctional cognition.

Coarse-graining network flow through statistical physics and machine learning. Nat Commun 16, 1605 (2025)
Zhang zhang, Arsham Ghavasieh, Jiang Zhang, Manlio De Domenico
We use graph neural networks to identify suitable groups of components for coarse-graining a network and achieve a low computational complexity, suitable for practical application. Our approach preserves information flow even under significant compression, as shown through theoretical analysis and experiments on synthetic and empirical networks. We find that the model merges nodes with similar structural properties, suggesting they perform redundant roles in information transmission. This method enables low-complexity compression for extremely large networks, offering a multiscale perspective that preserves information flow in biological, social, and technological networks better than existing methods mostly focused on network structure.

Dynamical reversibility and a new theory of causal emergence based on SVD. npj Complex 2, 3 (2025)
Jiang Zhang, Ruyi Tao, Keng Hou Leong, Mingzhe Yang, Bing Yuan
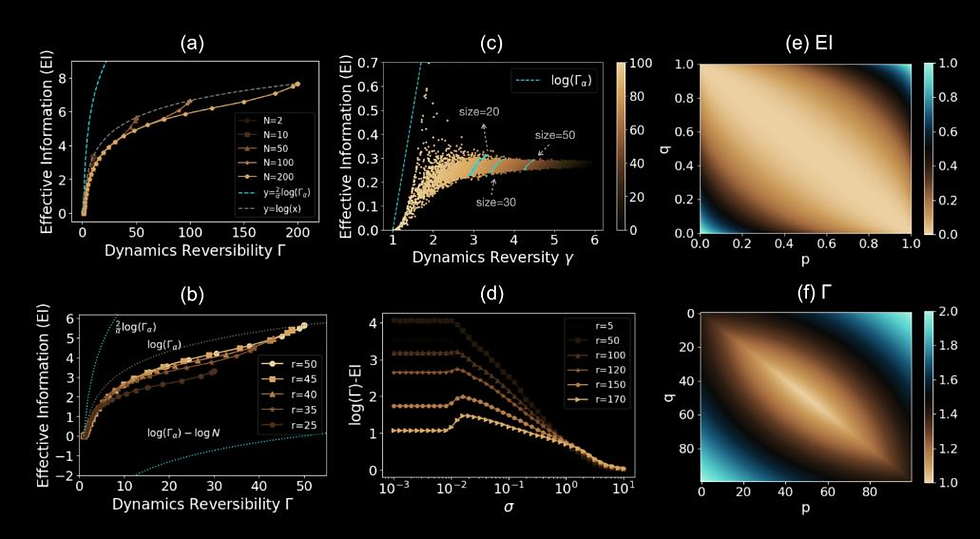
The theory of causal emergence based on effective information(EI) suggests that complex systems may exhibit a phenomenon called causal emergence(CE), where the macro-dynamics demonstrate a stronger causal effect than the microdynamics. We present an innovative approach to quantifying CE that is agnostic to specific coarse-graining techniques and effectively captures the inherent characteristics of Markov dynamics. Through empirical evaluations on examples of boolean networks, cellular automata, and complex networks, we validate our refined CE definition.
Dynamical reversibility and a new theory of causal emergence based on SVD. npj Complex 2, 3 (2025)
Jiang Zhang, Ruyi Tao, Keng Hou Leong, Mingzhe Yang, Bing Yuan
The theory of causal emergence based on effective information(EI) suggests that complex systems may exhibit a phenomenon called causal emergence(CE), where the macro-dynamics demonstrate a stronger causal effect than the microdynamics. We present an innovative approach to quantifying CE that is agnostic to specific coarse-graining techniques and effectively captures the inherent characteristics of Markov dynamics. Through empirical evaluations on examples of boolean networks, cellular automata, and complex networks, we validate our refined CE definition.

Model predictive complex system control from observational and interventional data. Chaos 34, 093125 (2024)
Muyun Mou, Yu Guo, Fanming Luo, Yang Yu, Jiang Zhang
We introduce a two-stage model predictive complex system control framework, comprising an offline pre-training phase that leverages rich observational data to capture spontaneous evolutionary dynamics and an online fine-tuning phase that uses a variant of model predictive control to implement intervention actions. To address the high-dimensional nature of the state-action space in complex systems, we propose a novel approach employing action-extended graph neural networks to model the Markov decision process of complex systems and design a hierarchical action space for learning intervention actions. This approach performs well in three complex system control environments: Boids, Kuramoto, and Susceptible-Infectious-Susceptible (SIS) metapopulation. It offers accelerated convergence, robust generalization, and reduced intervention costs compared to the baseline algorithm. This work provides valuable insights into controlling complex systems with high-dimensional state-action spaces and limited intervention data, presenting promising applications for real-world challenges.

Finding emergence in data by maximizing effective information. National Science Review, 2024, nwae279
Mingzhe Yang, Zhipeng Wang, Kaiwei Liu, Yingqi Rong, Bing Yuan, Jiang Zhang
Inspired by the theory of causal emergence (CE), this paper introduces a machine learning framework to learn macro-dynamics in an emergent latent space and quantify the degree of CE. The framework maximizes effective information, resulting in a macro-dynamics model with enhanced causal effects. Experimental results on simulated and real data demonstrate the effectiveness of the proposed framework. It quantifies degrees of CE effectively under various conditions and reveals distinct influences of different noise types. It can learn a one-dimensional coarse-grained macro-state from fMRI data, to represent complex neural activities during movie clip viewing. Furthermore, improved generalization to different test environments is observed across all simulation data.

An Exact Theory of Causal Emergence for Linear Stochastic Iteration Systems. Entropy 2024, 26(8), 618
Kaiwei Liu, Bing Yuan, Jiang Zhang
In this study, we introduce an exact theoretic framework for causal emergence within linear stochastic iteration systems featuring continuous state spaces and Gaussian noise. Building upon this foundation, we derive an analytical expression for effective information across general dynamics and identify optimal linear coarse-graining strategies that maximize the degree of causal emergence when the dimension averaged uncertainty eliminated by coarse-graining has an upper bound. Our investigation reveals that the maximal causal emergence and the optimal coarse-graining methods are primarily determined by the principal eigenvalues and eigenvectors of the dynamic system’s parameter matrix, with the latter not being unique.

Emergence and Causality in Complex Systems: A Survey of Causal Emergence and Related Quantitative Studies. Entropy 2024, 26(2), 108
Bing Yuan, Jiang Zhang, Aobo Lyu, Jiayun Wu, Zhipeng Wang, Mingzhe Yang, Kaiwei Liu, Muyun Mou, Peng Cui
This paper provides a comprehensive review of recent advancements in quantitative theories and applications of CE. It focuses on two primary challenges: quantifying CE and identifying it from data. The latter task requires the integration of machine learning and neural network techniques, establishing a significant link between causal emergence and machine learning. We highlight two problem categories: CE with machine learning and CE for machine learning, both of which emphasize the crucial role of effective information (EI) as a measure of causal emergence. The final section of this review explores potential applications and provides insights into future perspectives.

Expectation-maximizing network reconstruction and most applicable network types based on binary time series data. Physica D: Nonlinear Phenomena
Kaiwei Liu, Xing Lü, Fei Gao, Jiang Zhang
Based on the binary time series data of social infection dynamics, we propose a general framework to reconstruct the 2-simplicial complexes with two-body and three-body interactions by combining the maximum likelihood estimation in statistical inference and introducing the expectation maximization. In order to improve the code running efficiency, the whole algorithm adopts vectorization expressions. Through the inference of maximum likelihood estimation, the vectorization expression of the edge existence probability can be obtained, and through the probability matrix, the adjacency matrix of the network can be estimated. The framework has been tested on different types of complex networks. Among them, four kinds of networks achieve high reconstruction effectiveness. Finally, we analyze which type of network is more suitable for this framework, and propose methods to improve the effectiveness of the experimental results. Complex networks are presented in the form of simplicial complexes. In this paper, focusing on the differences in the effectiveness of simplicial complexes reconstruction after the same number of iterations, we innovatively propose that simplex reconstruction based on maximum likelihood estimation is more suitable for small-world networks and three indicators to judge the structural similarity between a network and a small-world network are given. The closer the network structure to the small-world network is, the higher efficiency in a shorter time can be obtained.
Finding emergence in data by maximizing effective information. arXiv:2308.09952 [physics.soc-ph]
Mingzhe Yang, Zhipeng Wang, Kaiwei Liu, Yingqi Rong, Bing Yuan, Jiang Zhang
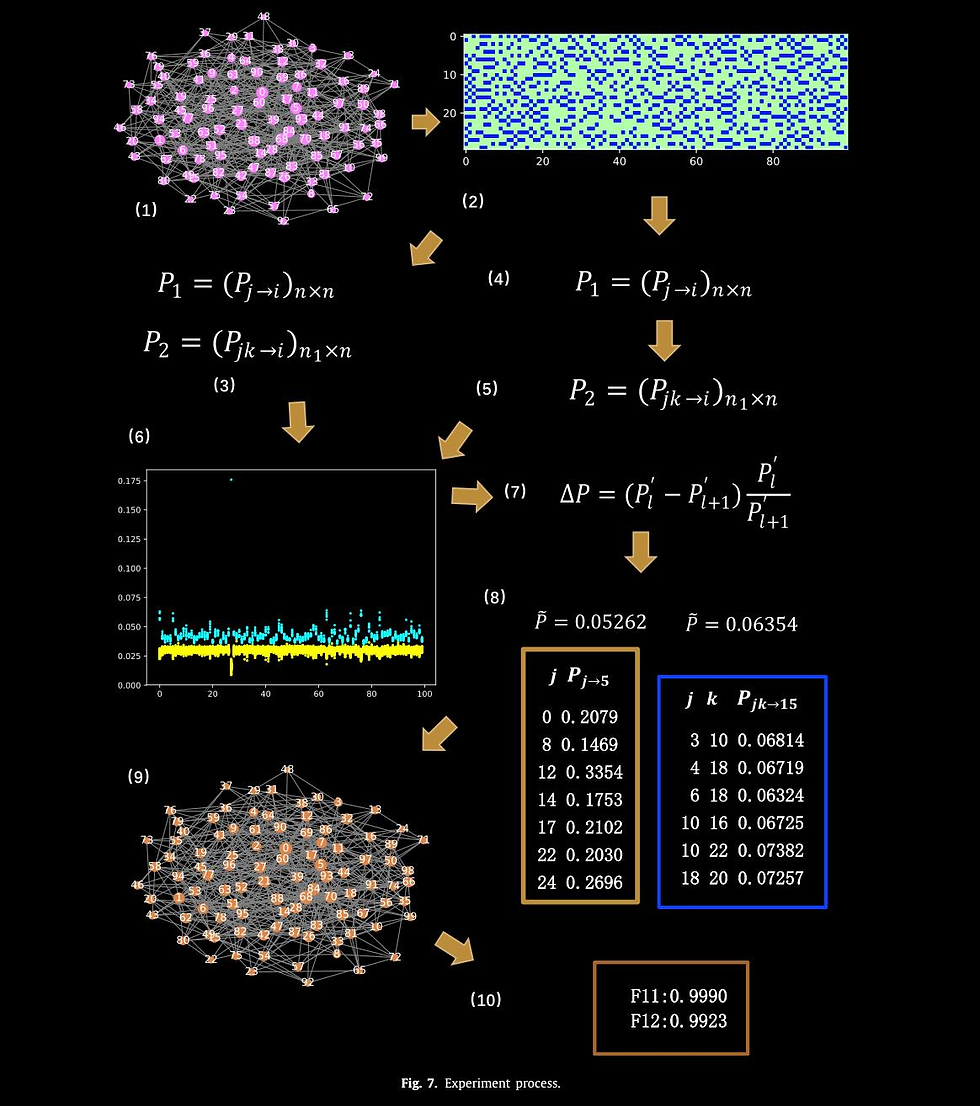
Inspired by the theory of causal emergence (CE), this paper introduces a machine learning framework to learn macro-dynamics in an emergent latent space and quantify the degree of CE. The framework maximizes effective information, resulting in a macro-dynamics model with enhanced causal effects. Experimental results on simulated and real data demonstrate the effectiveness of the proposed framework. It quantifies degrees of CE effectively under various conditions and reveals distinct influences of different noise types. It can learn a one-dimensional coarse-grained macro-state from fMRI data, to represent complex neural activities during movie clip viewing. Furthermore, improved generalization to different test environments is observed across all simulation data.

Finding emergence in data by maximizing effective information. arXiv:2308.09952 [physics.soc-ph]
Mingzhe Yang, Zhipeng Wang, Kaiwei Liu, Yingqi Rong, Bing Yuan, Jiang Zhang
Inspired by the theory of causal emergence (CE), this paper introduces a machine learning framework to learn macro-dynamics in an emergent latent space and quantify the degree of CE. The framework maximizes effective information, resulting in a macro-dynamics model with enhanced causal effects. Experimental results on simulated and real data demonstrate the effectiveness of the proposed framework. It quantifies degrees of CE effectively under various conditions and reveals distinct influences of different noise types. It can learn a one-dimensional coarse-grained macro-state from fMRI data, to represent complex neural activities during movie clip viewing. Furthermore, improved generalization to different test environments is observed across all simulation data.

Data Driven Modeling for Self-Similar Dynamics. arXiv:2310.08282 [cs.LG]
Ru-yi Taoa, Ning-ning Tao, Yi-zhuang You, Jiang Zhang
In this paper, we introduce a multiscale neural network framework that incorporates self-similarity as prior knowledge, facilitating the modeling of self-similar dynamical systems. For deterministic dynamics, our framework can discern whether the dynamics are self-similar. For uncertain dynamics, it not only can judge whether it is self-similar or not, but also can compare and determine which parameter set is closer to self-similarity. The framework allows us to extract scale-invariant kernels from the dynamics for modeling at any scale. Moreover, our method can identify the power-law exponents in self-similar systems, providing valuable insights for addressing critical phase transitions in non-equilibrium systems.

Neural Network Pruning by Gradient Descent. arXiv:2311.12526 [cs.LG]
Zhang Zhang, Ruyi Tao, Jiang Zhang
In this paper, we introduce a novel and straightforward neural network pruning framework that incorporates the Gumbel-Softmax technique. This framework enables the simultaneous optimization of a network’s weights and topology in an end-to-end process using stochastic gradient descent. Empirical results demonstrate its exceptional compression capability, maintaining high accuracy on the MNIST dataset with only 0.15% of the original network parameters. Moreover, our framework enhances neural network interpretability, not only by allowing easy extraction of feature importance directly from the pruned network but also by enabling visualization of feature symmetry and the pathways of information propagation from features to outcomes. Although the pruning strategy is learned through deep learning, it is surprisingly intuitive and understandable, focusing on selecting key representative features and exploiting data patterns to achieve extreme sparse pruning. We believe our method opens a promising new avenue for deep learning pruning and the creation of interpretable machine learning systems.

Learning nonequilibrium statistical mechanics and dynamical phase transitions. Nat Commun 15, 1117 (2024)
Nonequilibrium statistical mechanics exhibit a variety of complex phenomena far from equilibrium. It inherits challenges of equilibrium, including accurately describing the joint distribution of a large number of configurations, and also poses new challenges as the distribution evolves over time. Characterizing dynamical phase transitions as an emergent behavior further requires tracking nonequilibrium systems under a control parameter. While a number of methods have been proposed, such as tensor networks for one-dimensional lattices, we lack a method for arbitrary time beyond the steady state and for higher dimensions. Here, we develop a general computational framework to study the time evolution of nonequilibrium systems in statistical mechanics by leveraging variational autoregressive networks, which offer an efficient computation on the dynamical partition function, a central quantity for discovering the phase transition. We apply the approach to prototype models of nonequilibrium statistical mechanics, including the kinetically constrained models of structural glasses up to three dimensions. The approach uncovers the active-inactive phase transition of spin flips, the dynamical phase diagram, as well as new scaling relations. The result highlights the potential of machine learning dynamical phase transitions in nonequilibrium systems.
Tensor networks for unsupervised machine learning. Phys. Rev. E 107, L012103
Jing Liu, Sujie Li, Jiang Zhang, Pan Zhang
Modeling the joint distribution of high-dimensional data is a central task in unsupervised machine learning. In recent years, many interests have been attracted to developing learning models based on tensor networks, which have the advantages of a principle understanding of the expressive power using entanglement properties, and as a bridge connecting classical computation and quantum computation. Despite the great potential, however, existing tensor network models for unsupervised machine learning only work as a proof of principle, as their performance is much worse than the standard models such as restricted Boltzmann machines and neural networks. In this Letter, we present autoregressive matrix product states (AMPS), a tensor network model combining matrix product states from quantum many-body physics and autoregressive modeling from machine learning. Our model enjoys the exact calculation of normalized probability and unbiased sampling. We demonstrate the performance of our model using two applications, generative modeling on synthetic and real-world data, and reinforcement learning in statistical physics. Using extensive numerical experiments, we show that the proposed model significantly outperforms the existing tensor network models and the restricted Boltzmann machines, and is competitive with state-of-the-art neural network models.
Neural Network Pruning by Gradient Descent. arXiv:2311.12526 [cs.LG]
Zhang Zhang, Ruyi Tao, Jiang Zhang
In this paper, we introduce a novel and straightforward neural network pruning framework that incorporates the Gumbel-Softmax technique. This framework enables the simultaneous optimization of a network’s weights and topology in an end-to-end process using stochastic gradient descent. Empirical results demonstrate its exceptional compression capability, maintaining high accuracy on the MNIST dataset with only 0.15% of the original network parameters. Moreover, our framework enhances neural network interpretability, not only by allowing easy extraction of feature importance directly from the pruned network but also by enabling visualization of feature symmetry and the pathways of information propagation from features to outcomes. Although the pruning strategy is learned through deep learning, it is surprisingly intuitive and understandable, focusing on selecting key representative features and exploiting data patterns to achieve extreme sparse pruning. We believe our method opens a promising new avenue for deep learning pruning and the creation of interpretable machine learning systems.

Graph Completion Through Local Pattern Generalization. Complex Networks & Their Applications XII. COMPLEX NETWORKS 2023.
Zhang Zhang, Ruyi Tao, Yongzai Tao, Mingze Qi, Jiang Zhang
In this study, we introduce a model called C-GIN, which captures local structural patterns in the observed portions of a network using a Graph Auto-Encoder equipped with a Graph Isomorphism Network. This model generalizes these patterns to complete the entire graph. Experimental results on both synthetic and real-world networks across diverse domains indicate that C-GIN not only requires less information but also outperforms baseline prediction models in most cases. Additionally, we propose a metric known as “Reachable Clustering Coefficient (RCC)” based on network structure. Experiments reveal that C-GIN performs better on networks with higher Reachable CC values.

Evolutionary Tinkering Enriches the Hierarchical and Nested Structures in Amino Acid Sequences
Zecheng Zhang, Chunxiuzi Liu, Yingjun Zhu, Lu Peng, Weiyi Qiu, Qianyuan Tang, He Liu, Ke Zhang, Zengru Di, Yu Liu
Genetic information often exhibits hierarchical and nested relationships, achieved through the reuse of repetitive subsequences such as duplicons and transposable elements, a concept termed ``evolutionary tinkering'' by Fran\c{c}ois Jacob. Current bioinformatics tools often struggle to capture these, particularly the nested, relationships. To address this, we utilized Ladderpath, a new approach within the broader category of Algorithmic Information Theory, introducing two key measures: order-rate $\eta$ for characterizing sequence pattern repetitions and regularities, and ladderpath-complexity $\kappa$ for assessing hierarchical and nested richness. Our analysis of amino acid sequences revealed that humans have more sequences with higher $\kappa$ values, and proteins with many intrinsically disordered regions exhibit increased $\eta$ values. Additionally, it was found that extremely long sequences with low $\eta$ are rare. We hypothesize that this arises from varied duplication and mutation frequencies across different evolutionary stages, which in turn suggests a zigzag pattern for the evolution of protein complexity. This is supported by simulations and studies of protein families like Ubiquitin and NBPF, implying species-specific or environment-influenced protein elongation strategies. The Ladderpath approach offers a quantitative lens to understand evolutionary tinkering and reuse, shedding light on the generative aspects of biological structures.

Theoretical perspective on synthetic man-made life: Learning from the origin of life
Lu Peng, Zecheng Zhang, Xianyi Wang, Weiyi Qiu, Liqian Zhou, Hui Xiao, Chunxiuzi Liu, Shaohua Tang, Zhiwei Qin, Jiakun Jiang, Zengru Di, Yu Liu
Creating a man-made life in the laboratory is one of life science’s most intriguing yet challenging problems. Advances in synthetic biology and related theories, particularly those related to the origin of life, have laid the groundwork for further exploration and understanding in this field of artificial life or man-made life. But there remains a wealth of quantitative mathematical models and tools that have yet to be applied to this area. In this paper, we review the two main approaches often employed in the field of man-made life: the top-down approach that reduces the complexity of extant and existing living systems and the bottom-up approach that integrates well-defined components, by introducing the theoretical basis, recent advances, and their limitations. We then argue for another possible approach, namely “bottom-up from the origin of life”: Starting with the establishment of autocatalytic chemical reaction networks that employ physical boundaries as the initial compartments, then designing directed evolutionary systems, with the expectation that independent compartments will eventually emerge so that the system becomes free-living. This approach is actually analogous to the process of how life originated. With this paper, we aim to stimulate the interest of synthetic biologists and experimentalists to consider a more theoretical perspective, and to promote the communication between the origin of life community and the synthetic man-made life community.

Many dynamical processes of complex systems can be understood as the dynamics of a group of nodes interacting on a given network structure. However, finding such interaction structure and node dynamics from time series of node behaviors is tough. Conventional methods focus on either network structure inference task or dynamics reconstruction problem, very few of them can work well on both. This paper proposes a universal framework for reconstructing network structure and node dynamics at the same time from observed time-series data of nodes. We use a differentiable Bernoulli sampling process to generate a candidate network structure, and we use neural networks to simulate the node dynamics based on the candidate network. We then adjust all the parameters with a stochastic gradient descent algorithm to maximize the likelihood function defined on the data. The experiments show that our model can recover various network structures and node dynamics at the same time with high accuracy. It can also work well on binary, discrete, and continuous time-series data, and the reconstruction results are robust against noise and missing information.

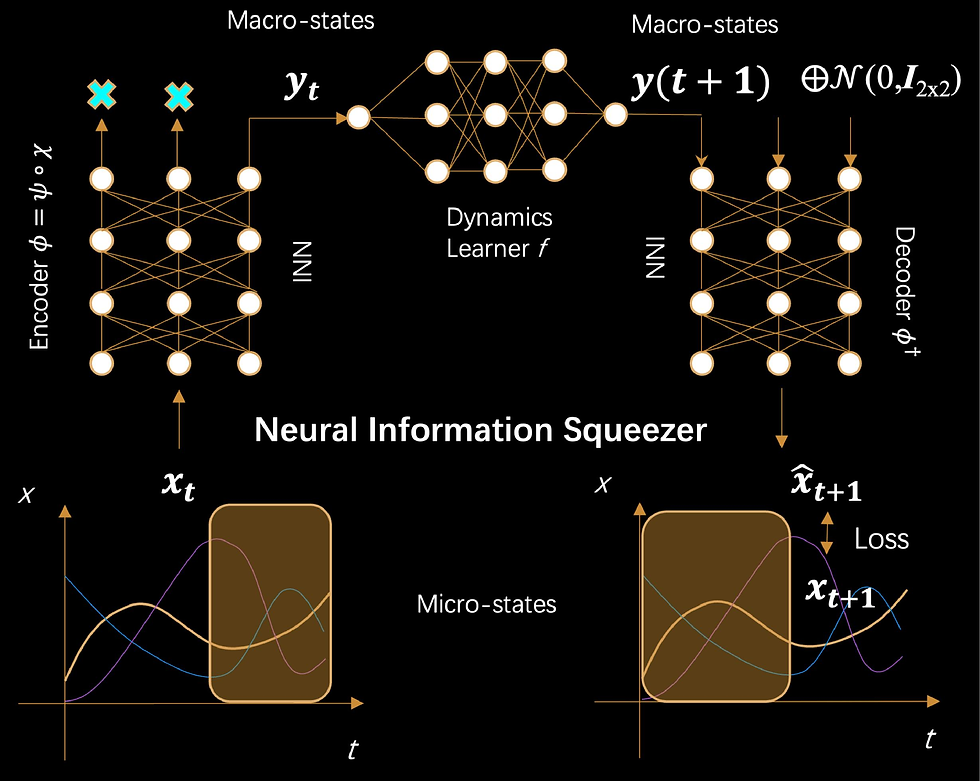
Conventional studies of causal emergence have revealed that stronger causality can be obtained on the macro-level than the micro-level of the same Markovian dynamical systems if an appropriate coarse-graining strategy has been conducted on the micro-states. However, identifying this emergent causality from data is still a difficult problem that has not been solved because the appropriate coarse-graining strategy can not be found easily. This paper proposes a general machine learning framework called Neural Information Squeezer to automatically extract the effective coarse-graining strategy and the macro-level dynamics, as well as identify causal emergence directly from time series data. By using invertible neural network, we can decompose any coarse-graining strategy into two separate procedures: information conversion and information discarding. In this way, we can not only exactly control the width of the information channel, but also can derive some important properties analytically. We also show how our framework can extract the coarse-graining functions and the dynamics on different levels, as well as identify causal emergence from the data on several exampled systems.